线性代数的本质:本质、以及第15集中的公理-线性代数十大法则
3665 2021-01-18 09:32 2025-11-26 10:58
线性变换:
- 直线在变换后仍然保持直线,不能有所弯曲(包括每个小网格的对角线延长线不能弯曲),我理解为空间匀称(各向平(间隔)直(无波动))
- 原点必需保持固定
什么是线性,不能升维,不能降维,比例不变; 对于数学的描述就是,直线不弯曲,对角线不弯曲,原点固定;升维就是1对多,降维就是多对一。
即保持网格线平行且等距分布的变换
标量:缩放(Scaling)——拉伸(stretching)或压缩(squishing)或反向(reversing)
向量:旋转(rotation)、剪贴(shear)x轴不变,y的单位从(0, 1)变到了(1, 1)
什么是向量,我认为,不管是在几维空间下,向量都是一组数,数组中的元素,每一个代表1维,如果能够分量相加满足点积,那么一定是正交。如果是正交,则彼此不受影响没有关联。这样的元素确定的一个量就是向量,那么确定了这样的量,一定是从原点出发。那么也就是观测者确立了一个,可以不是自身为原点但是大家都公认的参考系。由这样的向量,的维度,确立起来的下标,表示的线性变换方阵,如果是二维,就是张量,如果是二维以上,就是高阶张量。
ps、ai等作图软件:旋转、剪贴、镜像翻转
简而言之,这就是为什么妮阅读的每一本教科书都会根据可加性和成比例来定义线性变换。
而不是用网格线保持平行且等距分布来定义
对应1、5.结合律
2.交换律、注意这里的乘法没有交换律
7、8.分配律
德·摩根定律
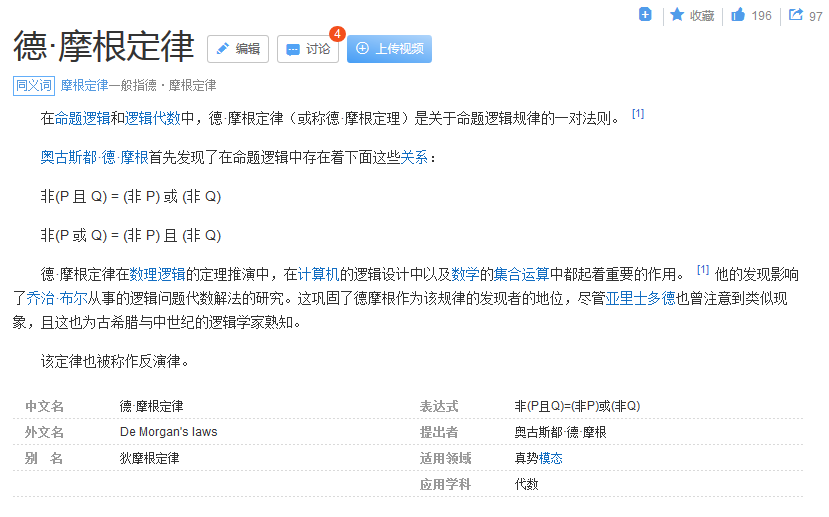
1、加法交换律:两数相加交换加数的位置,和不变。
2、加法结合律:三个数相加,先把前两个数相加,或先把后两个数相加,再同第三个数相加,和不变。
3、乘法交换律:两数相乘,交换因数的位置,积不变。
4、乘法结合律:三个数相乘,先把前两个数相乘,或先把后两个数相乘,再和第三个数相乘,它们的积不变。
5、乘法分配律:两个数的和同一个数相乘,可以把两个加数分别同这个数相乘,再把两个积相加,结果不变。
如:(2+4)×5=2×5+4×5
6、除法的性质:在除法里,被除数和除数同时扩大(或缩小)相同的倍数,商不变。 0除以任何不是0的数都得0。
简便乘法:被乘数、乘数末尾有0的乘法,可以先把0前面的相乘,零不参加运算,有几个零都落下,添在积的末尾。
7、什么叫等式?等号左边的数值与等号右边的数值相等的式子叫做等式。
等式的基本性质:等式两边同时乘以(或除以)一个相同的数,等式仍然成立。
8、什么叫方程式?答:含有未知数的等式叫方程式。
单项式:由数和字母的积组成的代数式叫做单项式,单独的一个数或一个字母也叫做单项式(例:0可看做0乘a,1可以看做1乘指数为0的字母,b可以看做b乘1),分数和字母的积的形式也是单项式。
多项式:在数学中,由若干个单项式相加组成的代数式叫做多项式(若有减法:减一个数等于加上它的相反数)。多项式中的每个单项式叫做多项式的项,这些单项式中的最高项次数,就是这个多项式的次数。其中多项式中不含字母的项叫做常数项。

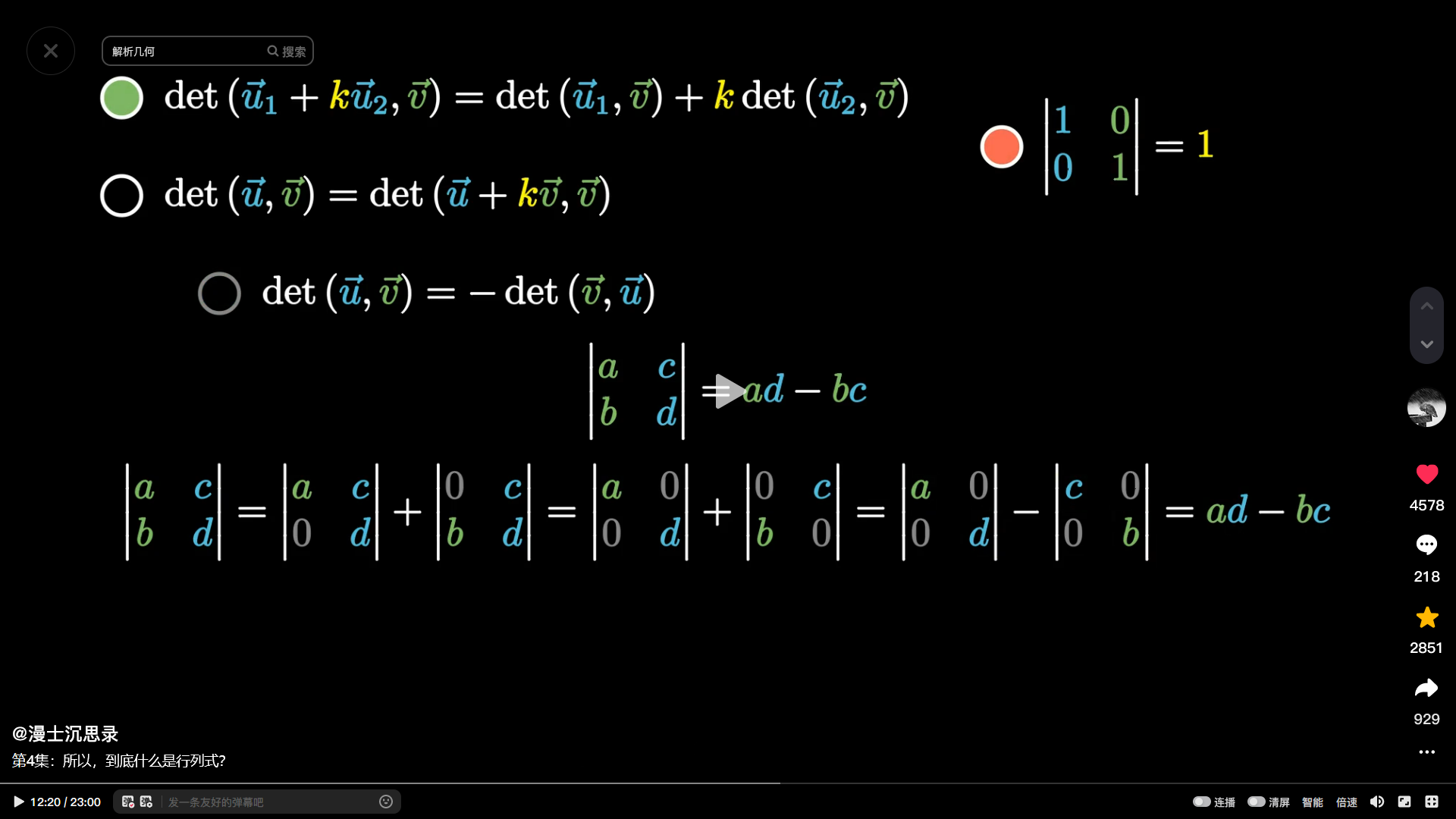
同济大学线性代数,你知道他是对的,但是你不知道他是怎么达到正确的,你也不知道他为什么会就这么想下去就对了。说明他没有告诉你他思考的过程,以及他碰到的问题,以及他一开始去的哪儿,因为什么去开了另一条路。最后收敛到了正确的路径上。你只是走了一遍他走过的路,但是丢失了他探索路上,最重要的吸取的教训和找到的规律的思维。方式。



全部评论